Linked Lists

A Linked List is a sequence of Nodes that are connected/linked to each other. The most defining feature of a Linked List is that each Node references the next Node in the link.

What’s a Linked List, Anyway? [Part 1]

One of the first things that we encounter when we learn about coding are data structures, which are the different ways that we can organize our data; variables, arrays, hashes, and objects are all types of data structures.
They are linear data structures, which means that there is a sequence and an order to how they are constructed and traversed. in order to get to the end of the list, we have to go through all of the items in the list in order, or sequentially.
The biggest differentiator between arrays and linked lists is the way that they use memory in our machines.
When an array is created, it needs a certain amount of memory. If we had 7 letters that we needed to store in an array, we would need 7 bytes of memory to represent that array. But, we’d need all of that memory in one contiguous block. That is to say, our computer would need to locate 7 bytes of memory that was free, one byte next to the another, all together, in one place.
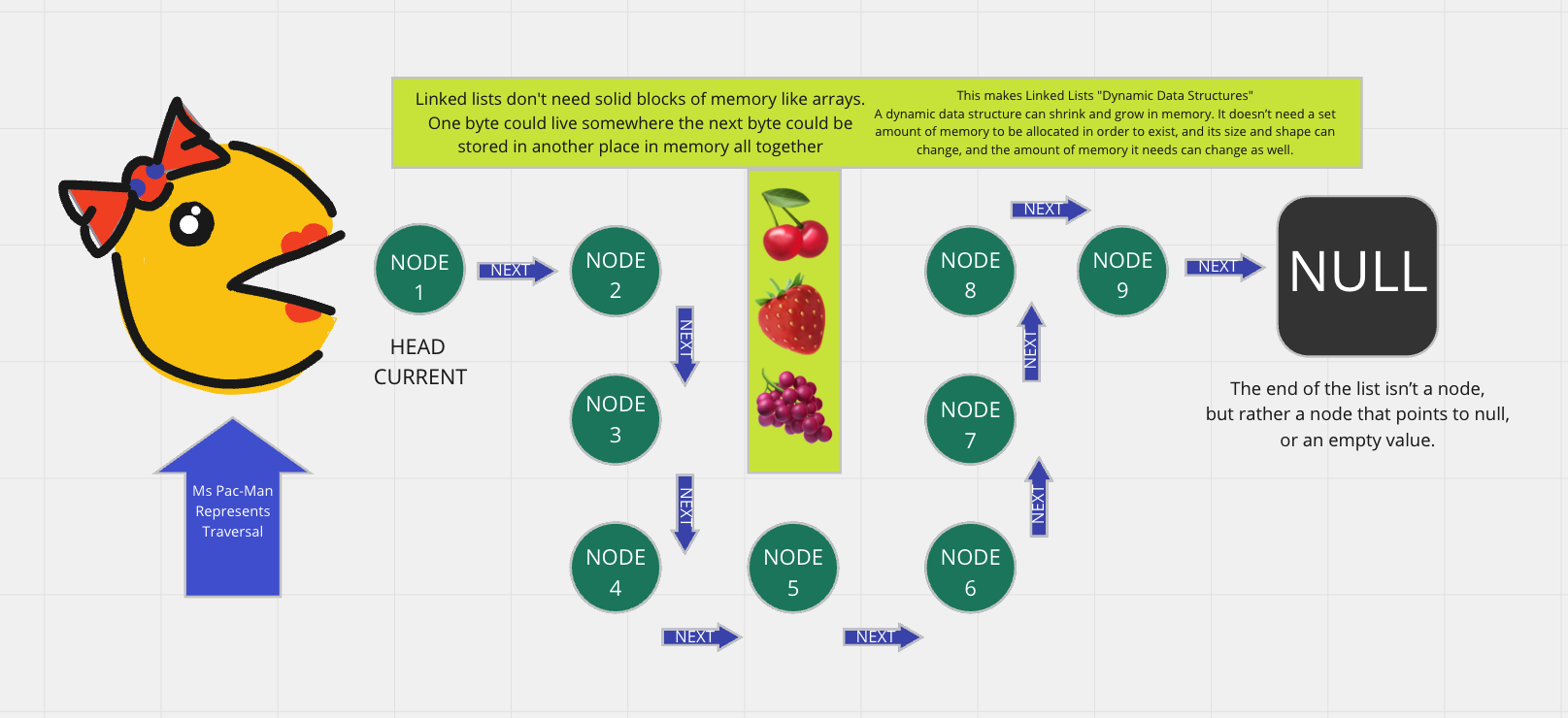
On the other hand, when a linked list is born, it doesn’t need 7 bytes of memory all in one place. One byte could live somewhere, while the next byte could be stored in another place in memory altogether! Linked lists don’t need to take up a single block of memory; instead, the memory that they use can be scattered throughout.
The fundamental difference between arrays and linked lists is that arrays are static data structures, while linked lists are dynamic data structures.
A static data structure needs all of its resources to be allocated when the structure is created; this means that even if the structure was to grow or shrink in size and elements were to be added or removed, it still always needs a given size and amount of memory.
a dynamic data structure can shrink and grow in memory. It doesn’t need a set amount of memory to be allocated in order to exist, and its size and shape can change, and the amount of memory it needs can change as well.
The starting point of the list is a reference to the first node, which is referred to as the head. Nearly all linked lists must have a head, because this is effectively the only entry point to the list and all of its elements
The end of the list isn’t a node, but rather a node that points to null, or an empty value.
A single node is also pretty simple. It has just two parts: data, or the information that the node contains, and a reference to the next node.
a single node has the “address” or a reference to the next node, they don’t need to live right next to one another, the way that the elements have to in an array. Instead, we can just rely on the fact that we can traverse our list by leaning on the pointer references to the next node, which means that our machines don’t need to block off a single chunk of memory in order to represent our list.

Singly linked lists are the simplest type of linked list, based solely on the fact that they only go in one direction. There is a single track that we can traverse the list in; we start at the head node, and traverse from the root until the last node, which will end at an empty null value.

Doubly linked list: has two references contained within each node: a reference to the next node, as well as the previous node. This can be helpful if we want to be able to traverse our data structure not just in a single track or direction, but also backwards.

A circular linked list is a little odd in that it doesn’t end with a node pointing to a null value. Instead, it has a node that acts as the tail of the list (rather than the conventional head node), and the node after the tail node is the beginning of the list. This organization structure makes it really easy to add something to the end of the list, because you can begin traversing it at the tail node, as the first element and last element point to one another.

What is a Linked List Anyway? Part 2

O(1) function takes constant time, which is to say that it doesn’t matter how many elements we have, or how huge our input is: it’ll always take the same amount of time and memory to run our algorithm.

O(n) function is linear, which means that as our input grows (from ten numbers, to ten thousand, to ten million), the space and time that we need to run that algorithm grows linearly.

O(n²) function, which clearly takes exponentially more time and memory the more elements that you have.

Grow a linked List, rearrange our pointers:

First, we find the head node of the linked list.
Next, we’ll make our new node, and set its pointer to the current first node of the list.
Lastly, we rearrange our head node’s pointer to point at our new node.

Inserting an element at the beginning of a linked list is particularly nice and efficient because it takes the same amount of time, no matter how long our list is, which is to say it has a space time complexity that is constant, or O(1).

Inserting an element at the end of a linked list:

Find the node we want to change the pointer of (in this case, the last node)
Create the new node we want to insert and set its pointer (in this case, to null)
Direct the preceding node’s pointer to our new node

Finding the last node means that we need to traverse through the entire linked list.

Because linked lists are distributed, non-contiguous memory so traversing is going to take time — it’s going to take more time with the more nodes we have.

The space time complexity this type of inserting will leave us with is a linear O(n). This insert algorithm would take as much time as the number of elements in our list

a linked list is usually efficient when it comes to adding and removing most elements, but can be very slow to search and find a single element.

If you ever find yourself having to do something that requires a lot of traversal, iteration, or quick index-level access, a linked list could be your worst enemy.
However, if you find yourself wanting to add a bunch of elements to a list and aren’t worried about finding elements again later, or if you know that you won’t need to traverse through the entirety of the list, a linked list could be your new best friend.

Linked Lists Analogy as Ms Pac-Man

Linked List Repl